ECUACIÓN DE LA DIFUSIVIDAD

ECUACIÓN DE LA DIFUSIVIDAD

La siguiente, es la Ecuación de la Difusividad:

La ecuación de la difusividad es la combinación de las principales ecuaciones que describen el proceso físico del movimiento de fluido dentro del reservorio, combina la ecuación de continuidad (que es el principio de la conservación de la masa, y de aquí obtenemos el balance de materia), la ecuación de flujo (ecuación de Darcy) y la ecuación de estado (compresibilidad).

Esta ecuación tiene 3 variables: 1 presión que es la del reservorio y 2 saturaciones que son generalmente la oil y la de gas en reservorios volumétricos.

A partir de esta ecuación se obtienen las ecuaciones para los tipos de flujo que existen en el reservorio, por ejemplo en la segunda parte de la ecuación de la difusividad la presión varia con el tiempo (deltaP/Delta t) si estamos en el estado pseudoestable es decir la presión no depende del tiempo ya que llego al limite del reservorio (infinit acting) esta variación es 0 por lo que la ecuación de la difusividad tendrá una resolución que es la ecuación de flujo radial para el estado pseudoestable:

Pr - Pwf = Costante*Q*uo*Bo(ln(re/rw)-0.75+S)/kh

A continuación se contempla el desarrollo de la ecuación de difusividad para el análisis de presión en yacimientos. El enfoque matemático que se presenta a continuación esta basado en los cursos PE175 (Well Test Analysis) y PE281 (Applied Mathematics for Reservoir Engineering) del programa de MS en Petroleum Engineering de Stanford University.

DESARROLLO DE LA ECUACION DE DIFUSIVIDAD
En un sistema lineal como se muestra en la figura:

La ecuación de conservación de la masa es:

(Masa entra) - (masa sale) = (acumulación)

dividiendo (1) por Dx y Dt, y tomando límites cuando Dx-->0 y Dt-->0:

sustituyendo la Ley de Darcy, ecuación (2), en (3) obtenemos:

suponiendo que k, m y A son constantes:

desarrollando el término:obtenemos: Ahora necesitamos calcular

Procedemos como sigue:

Primero tenemos que la compresibilidad isotérmica está definida como:

obtenemos:

derivando (7) con respecto al tiempo, obtenemos:

Por otro lado, la compresibilidad de la roca esta definida por:

Integrando (9) y derivando con respecto al tiempo, obtenemos:


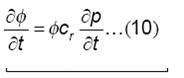
Sustituyendo (8) y (10) en (5), obtenemos:




Definiendo

obtenemos: Ahora, podemos decir que: Finalmente obtenemos: La ecuación (13) es la ecuación de difusividad en un sistema lineal.
Observe que en esta ecuación hay una derivada parcial con respecto al
tiempo y una segunda derivada con respecto a la distancia (espacio).
En un sistema cartesiano 3D, la ecuación (13) se puede escribir como
sigue:
donde, el operador V esta definido por:



En coordenadas radiales, el operador V esta definido por:


y la ecuación de difusividad se convierte en:




Si consideramos que solo existe flujo radial, la ecuación (15) se
convierte en:
Observe que en la derivación de la ecuación de difusividad (14) se requirió el uso de la ecuación de conservación de la masa (1), la Ley de Darcy (3) y las ecuaciones de estado (6) y (9).

El resultado es la ecuación general que caracteriza el comportamiento de presión en un yacimiento para todo tiempo. Las suposiciones que se han hecho son las siguientes:

1. Flujo laminar
2. Efectos capilares despreciables
3. Medio isotrópico
4. k, f, m y ct son constantes
5. Los fluidos son ligeramente compresibles
6. Flujo monofásico
7. No hay efectos de gravedad o térmicos